선형칼만필터 (4)
in Kalman on Kalman
칼만필터는 예측단계와 추정(업데이트) 두개의 시퀀스를 가지는 필터이다.
- 대충 이전의 데이터를 가지고 다음에 들어올 입력값을 예상해놓는다 (예측단계)
1.5 예측값의 분산의 계산 (공분간 계산단계)- 입력이 들어왔다. (관측)
- 입력데이터와 예측데이터를 비교해서 최적의 출력값을 추정 (업데이트 단계)
이번글에서는 업데이트에 관한 이야기를 해보겠다.
칼만게인
다시 관측 모델로 돌아가 보겠다.
실제 우리한테 계측 되는 데이터라는것은 실제의 데이터에 관측 행렬을 곱한 값과 같다.
z_k = H_k x_k + v_k또한 노이즈도 v_k로써 들어간다고 했다.
이제 우리들은, 앞서 설명하 칼만추정식에 관측 모델의 식을 대입해 볼려고 한다.
\hat{x}_k(+) = \hat{x}_k(-) + K_k[z_k - H\hat{x}_k(-)]여기에다가, 관측 모델을 입력하면
\hat{x}_k(+) = \hat{x}_k(-) + K_k[H_kx_k - H\hat{x}_k(-) + v_k]이런 모양이 된다는 것을 알 수있다.
그런데 한가지 빼먹은 것이 있다.
칼만게인은 어떻게 구하나요?
맞다. 우리는 아직 칼만게인을 구한적이 없다.
그렇다면 우리는 이 칼만게인을 어떻게 구하면 잘 구했다고 소문이 날까?
먼저, 우리는 진치는 죽었다가 깨어나도 알지 못한다.
그래서 우리들은 바로 진치와 추정치의 오차를 줄이지는 못하지만
그 오차의 분산을 최소한으로 할 수는 있다.
5/6 완료.
추정치와 진치의 오차의 공분산행렬
자 마지막이다.
추정치와 진치의 오차를 다음과 같이 쓸 수있다.
e=\hat{x}_k(+) - x_k다음으로 분산을 계산한다.
분산의 식에 집어넣으면 다음과 같이 쓸 수있다.
P_k(+) = \mathbb{E}(ee^\text{T}) = \mathbb{E}[(\hat{x}_k(+)-x_k)(\hat{x}_k(+)-x_k)^\text{T}]여기서 여러분들은 깨달아야한다.
이제는 P_k(+) 이구나 하고 알수있어야한다.
관측모델을 포함하는 칼만추정식은 다음과 같았다.
\hat{x}_k(+) = \hat{x}_k(-) + K_k[H_kx_k - H\hat{x}_k(-) + v_k]따라서
P_k(+) = \mathbb{E}\big[[(I-K_kH)(x_k-\hat{x}_k(-))-K_kv_k][(I-K_kH)(x_k-\hat{x}_k(-))-K_kv_k]^\text{T}\big]라는것을 잠깐만 펜을 굴려서 확인해보자
그러면 아래의 식을 확인 할 수있을것이다 (몰라도 괜찮다).
P_k(+) = P_k(-) - K_kH_kP_k(-) - P_k(-)H_k^\text{T}K_k^\text{T} + K_k(HP_k(-)H^\text{T} + R_k)K_k^\text{T}여기서, 공분산행렬 P_k 의 생김새를 보고 들어가자.
P_k =
\begin{bmatrix}
\sigma_r^{2} & 0\\
0 & \sigma_v^{2}
\end{bmatrix}\sigma_r^{2} 는 거리의 오차분산이고, \sigma_v^{2} 는 속도의 오차분산이다.
왜 대각행렬인가요?
여기서는 거리측정과 속도측정은 독립이라고 가정한다.
따라서 공분산이 없으므로
\sigma_r^{2}\sigma_v^{2} =0엥 어짜피 계산하기전에도 대각행렬이면, 대각성분만 계산하면 되겠네요?
맞다.
우리들의 목표는 추정치와 진치의 오차공분산행렬인 P_k 의 크기를 최소화하는 것이다.
따라서, trace 함수라는것을 사용한다.
trace함수는 대각성분의 합의 함수다.
대각성분의 스칼라 합을 미분을 취한후, 그 1차 미분이 0이되는 부분을 취하면, 최소지점을 찾을 수 있을것이라고 생각한다.
\dfrac{d \text{tr}(P_k)}{dK_k} = -2(H_kP_k(-))^\text{T} + 2K_k(H_kP_k(-)H_k^\text{T}+R_k)=0trace함수를 취하면 좋은점이, 행렬이 스칼라가 되어버리므로, 행렬의 특성상 순서가 중요했는데, 이제는 숫자에 불과하므로 식이 너무 간단해 진 것을 알 수있다.
그래서 저거를 0으로 만드는 K_k 를 계산을 한다면
K_k = P_{k}(-)H_{k}^\text{T}[H_kP_k(-)H_k^\text{T} + R_k]^{-1}요게된다.
자 내가항상 강조하는것은, 수식을 다 이해하는게 장땡은 아니다.
모르겠어도 형태라던지 흐름을 읽어야한다.
그래서 칼만 게인을 내가 볼때는 이렇게 읽는다.
K_k = \dfrac{P_{k}(-)H_{k}^\text{T}}{H_kP_k(-)H_k^\text{T} + R_k}근데 뭐라고?
H = 1이라고 했다.
K_k = \dfrac{P_{k}(-)}{P_k(-) + R_k}걍 이거다.
쉽게 쉽게 생각하면 추정치와 진치와의 오차공분산을 최소로하는것은 칼만게인의 분모에 측정오차를 계속 더해주면서 갱신하면된다는 소리다.
마치며
밑의 그림을 보고 잘 이해를 해보자.
의미를 밝혀적기위해, 한자로 써봣다.
왼쪽부터 오른쪽으로 읽어보자.
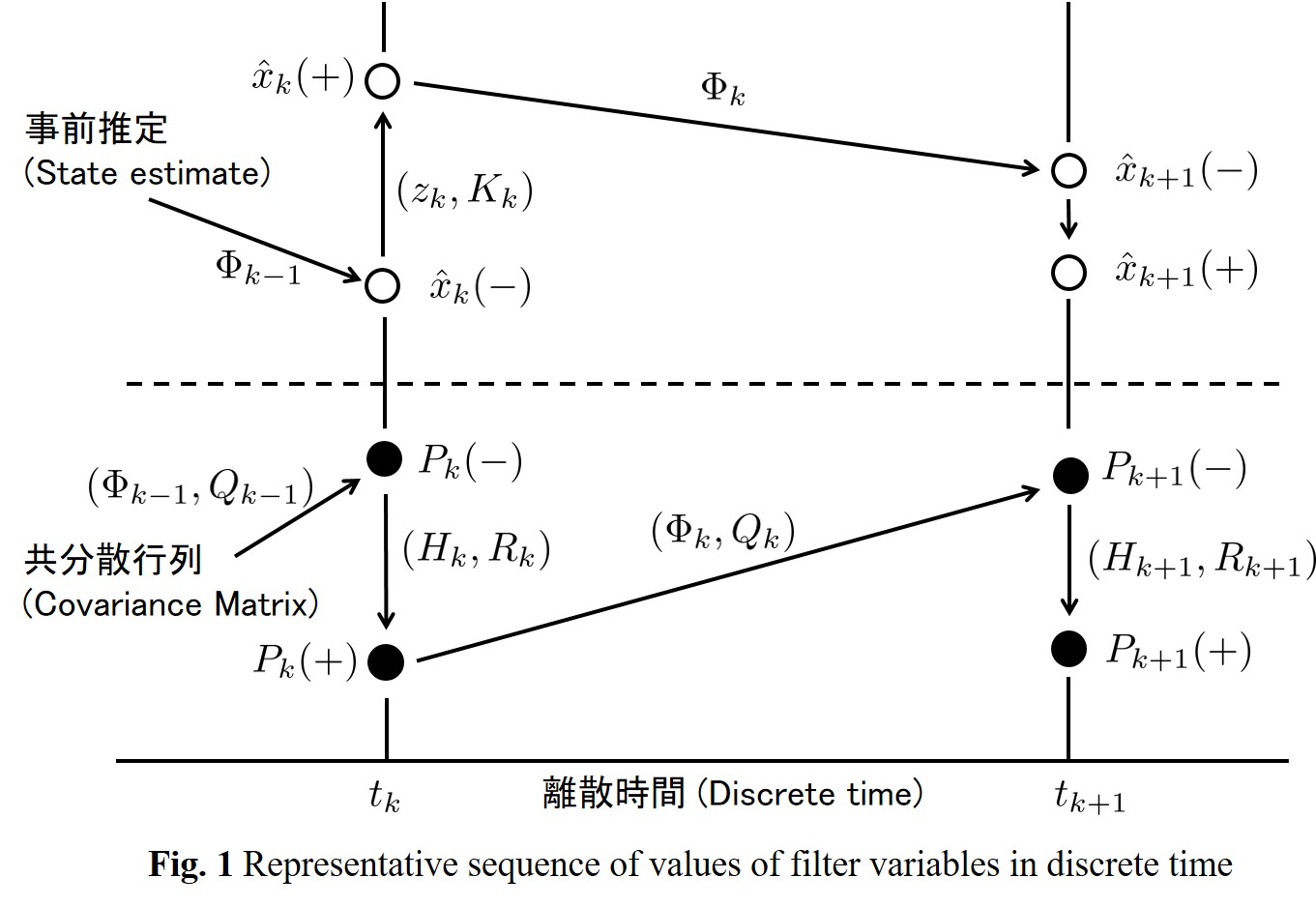
수식정리

알고리즘 정리
